Pattern Search Boyers Moore

Search a pattern in text of 10M characters in less than 2 seconds

String pattern match is one of the most prominent problem in computer science and has various applications like plagarism, document search, DNA match etc One of the frequently, used algorithm for pattern search is Boyer's Moore Algorithm which search for a pattern in a given string in BigO(n+m) time.

For pattern search using Boyer's Moore Algorithm, it is two phase process.

1. First, we need to preprocess the pattern
2. Implementing the Boyer's Moore Algorithm and use the preprocessed pattern above for alignment.

Today, I will briefly explain the Boyer's Moore Algorithm and discuss more about the different ways ( two ways ) of pre processing the pattern, which impacts how many characters we can skip while finding the pattern.

Brief of Boyer's Moore Algorithm Suppose we have a string GCAATGCCTATGTGACC and the pattern to search is TATGTG

Pattern search by Naive algorithm Big O(n^2)

If someone ask us to search a pattern in the string then we usually go via naive algorithm wherein we place the pattern at the beginning of the string and try to match all characters from left to right like below.

If it does not match, we slide the pattern one more character and then try to match like below.

We keep on doing that until, we found the pattern in the string or string is search completely and pattern is not found.

The time complexity of naive algorithm is Big O( n^2) and search for a pattern may takes upto days if a string is of millions of characters usually in the case of DNA sequence matching ( 3 Billion characters matched usually ) or detecting the plagrism in thousands of thousands docs.

Here comes the optimised algorithms like Boyer's Moore algorithm, Rabin Karp Algorithm, Knuth Algorithm etc.

Understanding the Boyer's Moore algorithm

There are two important steps of pattern matching with Boyer's Moore algorithm

1. Pattern will be matched from right to left, instead of left to right like in naive algorithm
2. Algorithm try to align the pattern in the string as much as possible unlike naive algorithm where it just keep on moving on character by character
   1. While matching from right to left, when we encounter the character which is bad character then
      1. Check if bad character exists in the pattern, if yes then shift the pattern toward right to align

Lets see how Boyer's Moore algorithm works

First we place the pattern at the beginning string and starts matching character by character from right to left. If all characters are matched then it is matched otherwise as you can see in the below screenshot, we will stop when we will found the character which does not matched i.e A.
Once we found the unmatched character A then we will try to find the unmatched character i.e. A in the pattern. If found then we will try to align the pattern accordingly. Thus, we skipped the 1 byte

Check the below screenshot, as we have aligned the pattern with the unmatched character. Once the pattern is aligned, we compare the characters from right to left again. As we start comparing character C is the unmatched character.

Now, we check if the unmatched character i.e C is present in the string from right to left in the pattern. As we can see it is not present in the string, so we will aligned the pattern past bad character i.e past C Hence, here we have skipped 5 bytes. Once the pattern is aligned, we again perform the comparison character by character. This time, we found the pattern. Check in below screenshot.

Hence, you can see, we are keep moving forward in the string to find the matched pattern. Hence, the pattern match algorithm is of ~ BigO(n) where n is the length of the string.

Boyer's Analysis

If you have noticed, then whenever there is a mismatched, then we have to check if the mismatched character does present in the string or not. To find that character we are traversing the pattern backwards i.e. right to left and from the position of the pattern where first mismatched has occured. This steps increase the complexity as we have to traverse all the way backward until that particular mismatched character is found or pattern is emptied, which makes the complexity of BigO(m) where m is the length of the pattern.
There are many ways, you can optimised the above step so that we do not have to traverse the whole pattern backward and somehow we can find whether that bad character is present in the pattern or not and if present then at what position it is present.

Here, I will provide two implementations

1. The first one, which is common and found on many academic websites, lets say it "array based pattern preprocessing"
2. The another one, which is found by me while optimising the algo further. Obviously, it might be already discovered somewhere by someone. Lets say it "hashmap based pattern preprocessing"

Array based pattern preprocessing

Lets assume we have a pattern AABCD, then one of the way is like this

1. Create the array of 256 char length say badChar[256] and initialize it with -1.
2. Traverse the pattern from left to right and at the ASCII position of a char write its position in the pattern like badChar[int(pattern[i])] = i

So basically, badChar array would be like this

Here, if you noticed then you will find that at index 65, we have written the position of right most A. Why is it so ? Consider the below use case

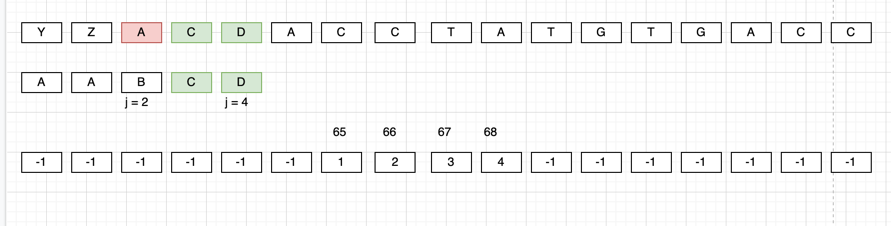
Now, using the badChar array, we can directly check if badChar[int(A)] == -1 then we can directly skip the whole pattern. Otherwise, if it is not -1 then the pattern need to be shift right by j - badChar[int(A)] bytes.

However, now consider the following case where we might face the issue or wrong number of shifts. Consider this pattern AABCDA, create the badChar array out of this

and consider this with matching the pattern

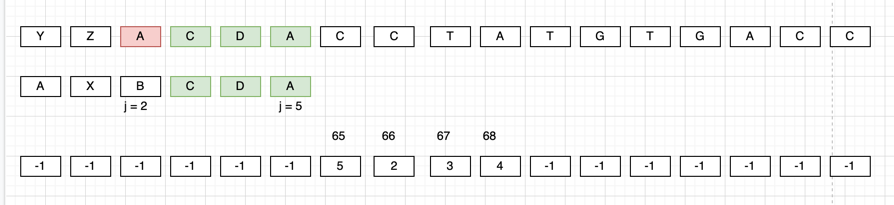
Here, we have got the bad character A so

1. First we will check if it even exists in the pattern or not, it can be done by badChar[int(A)].
2. As value is not -1, we need to determine the position of right most 'A' after the position of j. We wont be able to do it as while preprocessing we capture the right most A i.e at j = 5. Hence, algorithm will do the just one right shift, however if we see, ideally the shift should be of two bytes.

To circumvent this issue, we can do the preprocessing in the below way.

Hashmap based pattern preprocessing

In this method of preprocessing, we create the hashmap of characters in the pattern and the values would be the values at which all positions this particular char exists in the patter. Say we have a pattern AXBCDA then we will create the hashamp like this

A ---> [5, 0] 
X ---> [1]
B ---> [2]
C ---> [3]
D ---> [4]

Now consider the above scenario where it was failing when we used the array based preprocessing pattern.

Here, we have got the bad character A so

1. First we will check if it even exists in the pattern or not, it can be done by badChar.get("A").
2. As value is not null, we need to determine the position of right most 'A' after the position of j. we can simply do it by traversing the value of key A and we need to traverse until we find the first value less than the value of j and done.

By this method, for value of j = 2, we will get A at position 0, hence shift would be j - 0 = 2 instead of 1 that we were getting in the above method.

Caveats of the hashmap preprocessing

1. Use this preprocessing when pattern consist of varied number of characters like text search.
2. This preprocessing does not suit when pattern is consist of small number of characters like DNA sequence because it will make the value array too long and search within it would be of BigO(m) where m is the number of times a character x appear in pattern p.

Performance Analysis

For performance analysis, I use jprofiler.

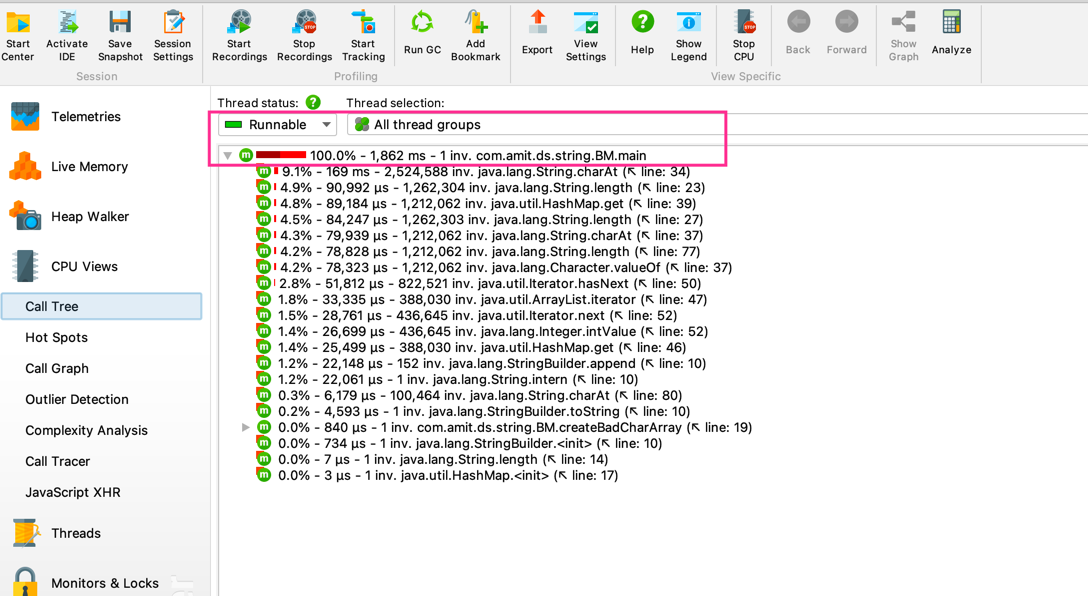
Test	String length	Pattern length	Time taken
1	10M characters	10000 characters	1.8ms

package com.amit.ds.string;


import java.util.*;

class BM{
    
public static void main(String args[]) {
        
//      Random characters can be generated from here https://onlinerandomtools.com/generate-random-string
        String inputString = "<ENTER_YOUR_10MB_Characters here>";
        
        String patternString = "xkbhntksfl";        
        
        int j = patternString.length() - 1;
        int i = 0;
        int index = i;
        HashMap<Character, ArrayList<Integer>> badChar = new HashMap<Character, ArrayList<Integer>>();
        
        createBadCharArray(patternString, badChar);
        int totalShift = 0;
        int totalLoop = 0;
        
        while( i < inputString.length()) {
                        
            totalLoop = totalLoop + 1;
            
            if ( i < ( patternString.length() - 1)) {
                
                
                i= i + 1;
                index = i;
            }
            
            else if ( inputString.charAt(index) != patternString.charAt(j)) {
                
                
                Character badCharacter = inputString.charAt(index);
                
                if(badChar.get(badCharacter) == null) {
                    
                    totalShift = totalShift + j + 1;
                    i = i + j + 1;
                }
                else {
                    
                    ArrayList<Integer> xArrayList = badChar.get(badCharacter);
                    Iterator<Integer> iterator = xArrayList.iterator();
                    int shift = 0;
                    
                    while(iterator.hasNext()) {
                        
                        int k = iterator.next();
                        
                        if (  k < j ) {
                            
                            shift = k;
                        }
                        else {
                            break;
                        }
                        
                    }
                    
                    totalShift =  j - shift ;
                    if (totalShift == 0) {
                        i= i + 1;
                    }
                    else {
                        i  = i + (j - shift );  
                    }
                    
                    
                }
                
                
                index = i;
                j = patternString.length() - 1;
                
            }
            else if(inputString.charAt(index) == patternString.charAt(j)) {
                

                index = index - 1;
                j= j- 1; 
                
                if ( j < 0 ) {
                    System.out.println("Pattern match found at index"  + (i - patternString.length() + 1));
                    j = patternString.length() - 1;
                    
                    i = i + 1;
                    index = i;
                    
                }
            }
        }
        
    }
    
    public static HashMap<Character, ArrayList<Integer>> createBadCharArray(String pattern, HashMap<Character, ArrayList<Integer>> badCharMap) {
        
        for ( int i=0; i< pattern.length(); i++) {
            ArrayList<Integer> xArrayList = badCharMap.get(pattern.charAt(i));
            
            if( xArrayList == null) {
                xArrayList =  new ArrayList<Integer>();
                xArrayList.add(i);
                badCharMap.put(pattern.charAt(i), xArrayList);
            }
            else {
                xArrayList.add(i);
                badCharMap.get(pattern.charAt(i));
            }
        }
        
        return badCharMap;
        
    }
//  public static int computeShift(String shiftPattern, String matchedPattern,  char badChar) {
//      
//      int shift =  0;
//      
//      for (int i=shiftPattern.length() -  1; i >= 0; i--) {
//          if (shiftPattern.charAt(i) == badChar) {
//              shift = shift + 1;
//              break;
//          }
//          else {
//              shift = shift + 1;
//          }
//      }
//      
//      if ( shift == 0) {
//          shift = shiftPattern.length();
//      }
//      
//      return shift + matchedPattern.length();
//      
//  }
     
    

}